Graph Theory
HNBGU MCA Previous Question Paper 2022
-
-
Discuss permutation and determine the number of permutations
that can be made out of the letters of the word
"PROGRAMMING".
-
Discuss combination and determine the number of triangles
that are formed by selecting points from a set of 15 points
out of which 8 are collinear.
-
-
Differentiate between homogeneous linear recurrence relation
and non-homogeneous linear recurrence relation. Discuss the
method used to solve the linear homogeneous recurrence
relation with constant coefficients.
-
Solve the recurrence relation Ar+2 - 5Ar+1 + 6Ar = 2 by the
method of generating functions satisfying the initial
conditions a0 = 1 and a1 = 2.
-
-
Define a connected graph. Prove that a connected graph with
n vertices has at least (n-1) edges.
-
Define the following:
- Planer graph
- Complete Bipartite graph
- Dual of a planer graph
Give one example each.
-
-
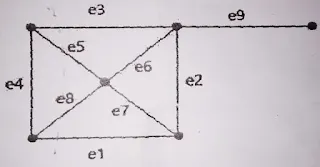
Check whether the two graphs are isomorphic or not. Justify
your answer.
-
Define Hamilton and Eulerian graphs. Prove the complete
graph K3,3 is Hamilton but not Eulerian.
-
-
Write short notes on the following:
- Tree and fundamental circuit.
- Rooted and Binary tree
- Various operation on graph
- Vector space of a graph
-
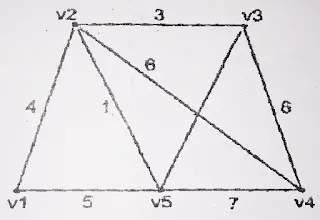
Discuss the Prim's algorithm. Using Prim's algorithm, find a
minimal spanning ttree for the weighted graph shown in the
following:
-
-
Define cut set. Find a cutsets of the graph G given below
and also find the edge connectivity of G:
-
Prove that a connected Planar graph with n vertices and e
edges has e-n+2 regions.
-
-
Differentiate between combinatorial and geometrical dual of
a graph. Draw the geoetric dual of the graph G given below.
-
Define Incidence matrix and Adjacency matrix of a directed
and undirected graph. Explain with suitable examples.
-
Write short notes on the following:
- Rule of sum and products.
- Coloring and covering partitioning of a graph
- Graph enumeration
- Four color problem
- Thickness and crossing of a graph









No comments:
Post a Comment